Bioinformatics 101 : Solving the Overlap Graphs Problem

Recently, I got back to expanding my PyBioinformatics repo. I thought I’d explain my approach to solving the issues posed on Rosalind (A bioinformatics teaching platform through problem solving).
In this blogpost, I’ll try to dissect and explain the “Overlap Graphs Problem”.

A Brief Introduction to Graph Theory

Networks arise everywhere in the practical world, especially in biology. Networks are prevalent in popular applications such as modeling the spread of disease, but the extent of network applications spreads far beyond popular science. Our first question asks how to computationally model a network without actually needing to render a picture of the network.

First, some terminology; graph is the technical term for a network; a graph is made up of hubs called nodes (vertices), pairs of which are connected via segments/curves called edges. If an edge connects nodes v and w, then it is denoted by v,w (or equivalently w,v).

- an edge v,w

is incident to nodes v and w; we say that v and w are adjacent to each other.

- the degree of v

is the number of edges incident to it.

- a walk

is an ordered collection of edges for which the ending node of one edge is the starting node of the next (e.g., {v1,v2} , {v2,v3} , {v3,v4} , etc.).

- a path

is a walk in which every node appears in at most two edges.

- a path length

is the number of edges in the path.

- a cycle

is a path whose final node is equal to its first node (so that every node is incident to exactly two edges in the cycle).

- the distance

between two vertices is the length of the shortest path connecting them.

Graph theory is the abstract mathematical study of graphs and their properties.

The Original Problem

A graph whose nodes have all been labeled can be represented by an adjacency list, in which each row of the list contains the two node labels corresponding to a unique edge.

An adjacency list is a two-column matrix that abstractly represents the edge relations of a graph without needing to physically draw the graph. Each row of the adjacency list encodes an edge {u,v} by placing u in the first column and v in the second column (or vice-versa). for example:

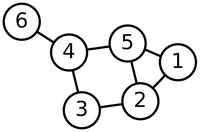
The adjacency list of this graph is given below (the rows could be given in any order, and the elements of any given row could be transposed).
|1, 2|
|1, 5|
|2, 3|
|2, 5|
|3, 4|
|4, 5|
|4, 6|

A directed graph (or digraph) is a graph containing directed edges, each of which has an orientation. That is, a directed edge is represented by an arrow instead of a line segment; the starting and ending nodes of an edge form its tail and head, respectively. The directed edge with tail v and head w is represented by (v,w) (but not by (w,v)). A directed loop is a directed edge of the form (v,v).

For a collection of strings and a positive integer k, the overlap graph for the strings is a directed graph Ok in which each string is represented by a node, and string s is connected to string t with a directed edge when there is a length k suffix of s that matches a length k prefix of t, as long as s≠t; we demand s≠t to prevent directed loops in the overlap graph (although directed cycles may be present).

Given: A collection of DNA strings in FASTA format having total length at most 10 kbp.

Return: The adjacency list corresponding to O3. We may return edges in any order.

Solution To The Problem

n.b For the sake of simplicity, I won’t explain how to parse FASTA files with python, you can check this simple explanation Parsing FASTA Files.

1.Approach
1.1 Parsing the Input:
The input is in FASTA format, where each sequence is prefixed with a label (e.g., >label1) followed by the DNA sequence. We have to extract the labels and their corresponding DNA sequences.

1.2 Identify Overlaps:
For each pair of strings s and t (where 𝑠 ≠ 𝑡) we check if the suffix of 𝑠 of length 𝑘 = 3 matches the prefix of t of length 𝑘=3.

1.3 Build the Adjacency List:

We represent each string as a node in the graph. If an overlap exists between s and t, we add a directed edge (s,t) to the adjacency list.

1.4 The Output:
We return the adjacency list, where each line contains a pair of labels representing a directed edge.

2.Algorithm
After extracting labels and sequences in the first step, we iterate through all pairs of sequences: For each sequence s, we extract its suffix of length 3.
For each sequence t, extract its prefix of length 3.
If the suffix of s matches the prefix of t, we add an edge from s to t.
We finally print the adjacency list.

3.Practical Python Code Implementation

def parse_fasta(data):
    """Parses FASTA formatted data into a dictionary of {label: sequence}."""
    sequences = {}
    label = None
    for line in data.strip().splitlines():
        if line.startswith(">"):
            label = line[1:]  # Extract label
            sequences[label] = ""
        else:
            sequences[label] += line.strip()  # Append sequence
    return sequences

def overlap_graph(sequences, k=3):
    """Generates the adjacency list for the overlap graph O_k."""
    adjacency_list = []
    labels = list(sequences.keys())
    
    for i, s_label in enumerate(labels):
        s_seq = sequences[s_label]
        s_suffix = s_seq[-k:]  # Get suffix of length k
        
        for j, t_label in enumerate(labels):
            if i != j:  # Ensure s != t
                t_seq = sequences[t_label]
                t_prefix = t_seq[:k]  # Get prefix of length k
                
                if s_suffix == t_prefix:  # Check for overlap
                    adjacency_list.append((s_label, t_label))
    
    return adjacency_list


""" Parse input and construct graph """
sequences = parse_fasta(data)
adj_list = overlap_graph(sequences, k=3)

""" Print adjacency list """
for edge in adj_list:
    print(edge[0], edge[1])
    

4.Complexity

Time Complexity: 𝑂(𝑛2), where 𝑛 is the number of sequences (checking all pairs).

Space Complexity: 𝑂(𝑛), to store the adjacency list.